PRONOM A theorem prover for nonnormal modal logics

by Tiziano Dalmonte, Sara Negri, Nicola Olivetti, and Gian Luca Pozzato, with the valuable help of Cyril Terrioux

A Prolog implementation of labelled sequent calculi for logic E and standard extensions with M, N, and C

Nonnormal modal logic:    E    EM    EM (opt)    EN    EC    EMN    EMC    ENC    EMNC   





Do NOT use capital letters for propositional variables.
Use: false for bottom, true for top, ^ for conjunction, ? for disjunction, - for negation, >> for material implication, box for modality ▢.

Examples
Valid formulas
(box (a ^ (b ? c))) >> (box ((a ^ b) ? (a ^ c)))
valid in E
(box(a ^ b)) >> (box(a))
axiom M
box true
axiom N
((box(a)) ^ (box(b))) >> (box(a ^ b))
axiom C
b >> (box (a >> a))
valid in N

Prolog Source Code

For all the systems: Utilities and Operators

To copy in the folder of source files
Operators
Utilities

Logic E

Characterizing axiom: -
Prolog Code

Logic EM

Characterizing axiom: M
(box(a ^ b)) >> ((box a) ^ (box b))
Prolog Code Prolog Code (optimized version)

Logic EN

Characterizing axiom: N
box true
Prolog Code

Logic EC

Characterizing axiom: C
((box a) ^ (box b)) >> (box(a ^ b))
Prolog Code

Logic EMN

Characterizing axioms: M and N
(box(a ^ b)) >> ((box a) ^ (box b))
box true
Prolog Code

Logic EMC

Characterizing axioms: M and C
(box(a ^ b)) >> ((box a) ^ (box b))
((box a) ^ (box b)) >> (box(a ^ b))
Prolog Code

Logic ENC

Characterizing axioms: N and C
box true
((box a) ^ (box b)) >> (box(a ^ b))
Prolog Code

Logic EMNC

Characterizing axioms: M, N and C
(box(a ^ b)) >> ((box a) ^ (box b))
box true
((box a) ^ (box b)) >> (box(a ^ b))
Prolog Code

Experiments

Prolog Code for executing tests

Statistics

Tests over valid formulas and over random formulas

The performances of PRONOM seems prmising. We have tested it:

  • on sets of valid formulas for each modal logic
  • on sets of randomly generated formulas, obtained by fixing the number of propositional variables, the depth (level of nesting of connectives) of a formula and a time limit.
To run tests:
  1. consult the Prolog source file of the system to be tested (e.g. e.pl)
  2. consult the Prolog source file of statistics
  3. to run tests over valid formulas, ask the Prolog engine to prove
    runValidFormulas(+system,+time_limit_in_seconds)
    where system can be: e, em, en, ec, enc, emn, emc, emnc
  4. to run tests over randomly generated formulas, ask the Prolog engine to prove
    runRandomFormulas(+number_of_tests,+number_of_propositional_variables,+depth,+time_limit_in_seconds)

Results of tests over valid formulas are shown in Table 1, whereas the percentage of timeouts in executing tests over randomly generated formulas are shown in Table 2.


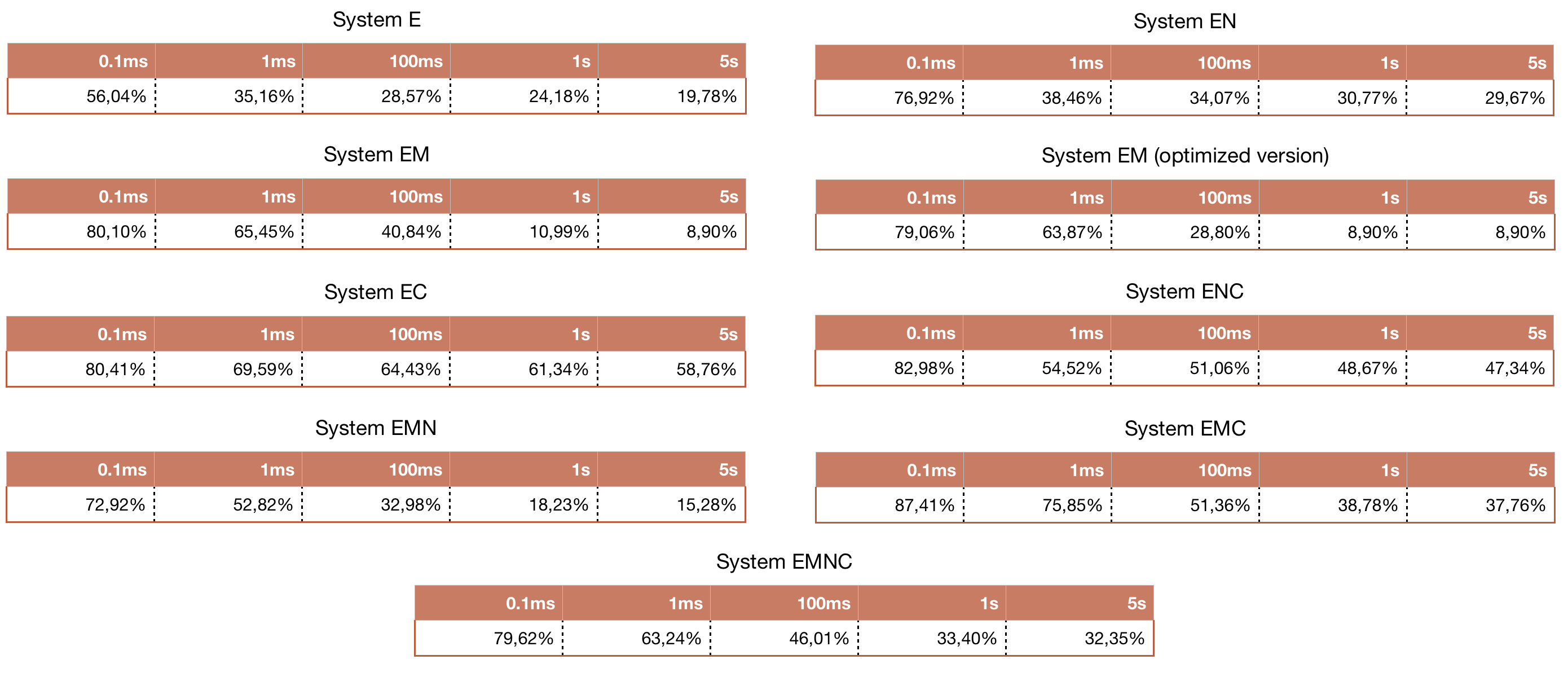
Table 1: percentage of timeouts of PRONOM over N valid formulas, 90 < N < 500.


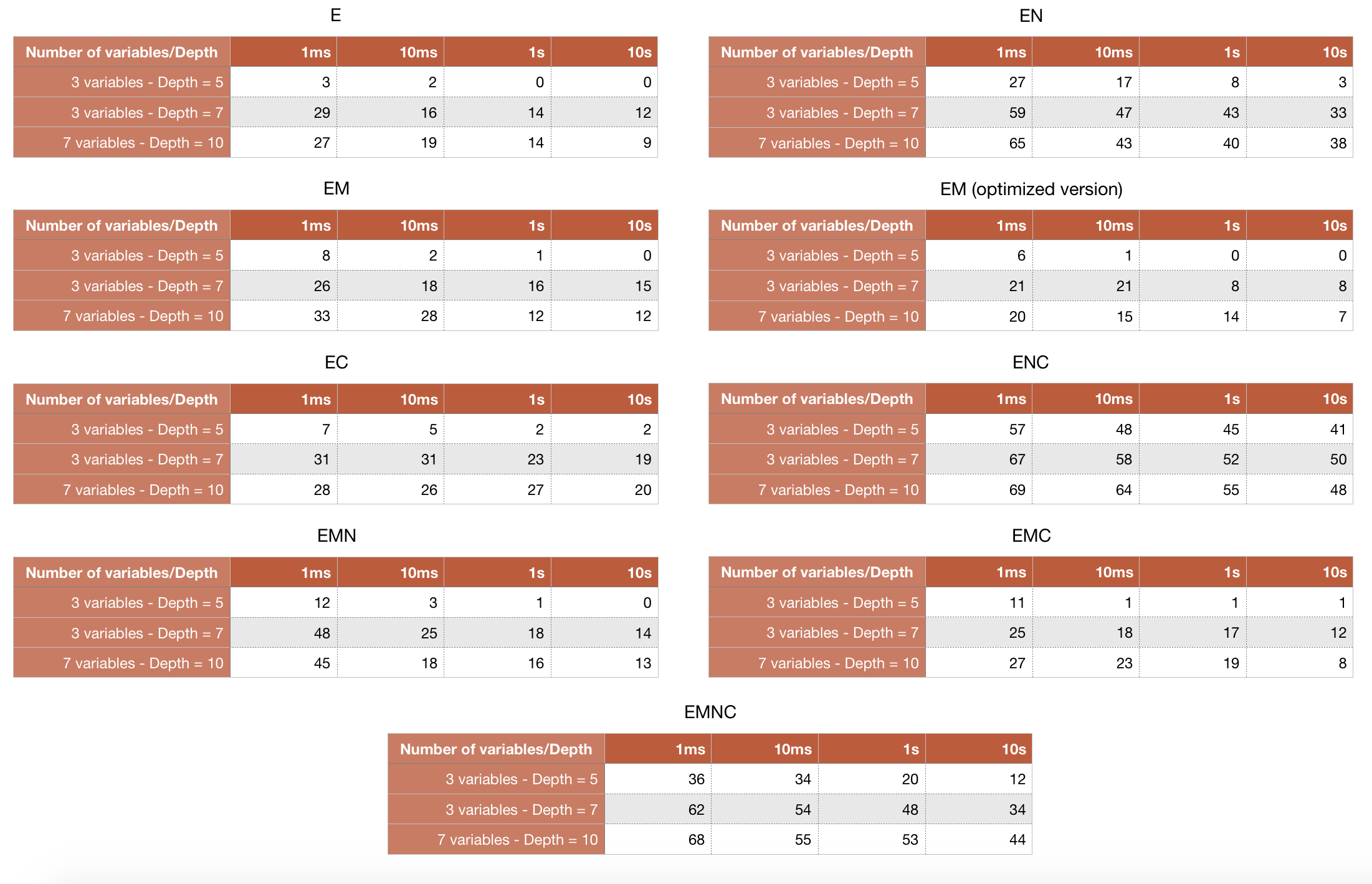
Table 2: percentage of timeouts of PRONOM over 8000 formulas randomly generated.

Contacts

Authors

Tiziano Dalmonte, Sara Negri,
Nicola Olivetti, Gian Luca Pozzato

with the valuable help of Cyril Terrioux
  • +39 011 670 68 48
  • gianlucapozzato